Kenneth Katzner's Languages of the World is being updated and since I'd reviewed the previous edition I'd been asked for comments on that and had my copy lying around. Browsing through it with Helen, she decided that Georgian was the most attractive script, so we transliterated and translated the first word (ღმერთსა / ghmertsa = to God) in the sample text, with the aid of Google Translate and Wikipedia. We're not about to learn Georgian, but I think she understands the difference between transliteration and translation now.
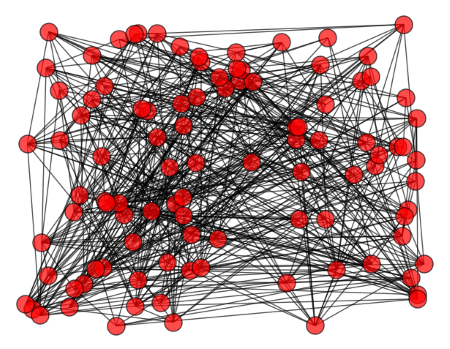
I was reading a post by John Cook on the spectra of random graphs and Helen asked me what the picture (right) was. So I explained what it was — an instance of G(100,0.1), it's a graph with 100 vertices and edges drawn with 0.1 probability — and we tried counting how many edges there were from some of the clearer vertices. (These are sometimes called Erdős-Rényi graphs, so I also got to explain that the Hungarian "double acute" is different to an umlaut.)
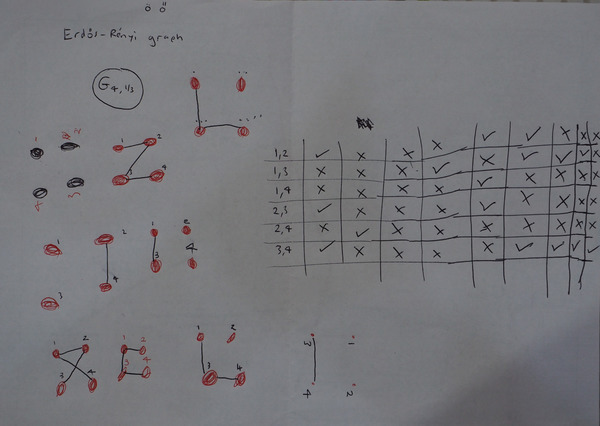
Then I had the idea that we could try doing this ourselves, for much smaller graphs, using pen and paper and dice. So we constructed nine instances of the random graph model G(4,⅓), rolling dice to do the selection.
I have no idea if Helen came away with any feel for the idea of a probability distribution over a space of graphs — and rolling two dice and adding them, generating a histogram, would seem a more straightforward introduction to non-uniform probability distributions — but she enjoyed the exercise, and insisted on generating two more graphs than I had planned on.
To be honest I don't think this makes much sense as a maths activity for six year olds but it's the kind of thing that happens when answering questions. And we had a lot of fun.